Difference between revisions of "MATLAB code"
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | =What are these files for?= | ||
| + | |||
| + | The find a good controller, you must find good gains values for the controller. This is easier said than done. The LQR function of matlab helps us to find the best gains values for two given cost matrices. But manually testing them is a lot of work, so the LQR file we have runs the LQR algorithm on many different cost matrix values and then also runs tests on each set of gains values to give you the best one possible. Running those tests requires a few different files. Once you have decided on a set of gains values that you want to explore more. You can run a singular test with those using runBicycleTest. The test will run telling you whether the bike fell or not, but it will also animate the bike and create multiple plots. This is needed to get a better insight on to how your controller is performing. When you have decided on a few different controllers you think perform well, you can run them individually and compare everything in detail, or you can run the plotMultipleControllersTogether file to run tests on those controllers and create plots comparing the controllers. | ||
| + | |||
| + | =How To Run Them= | ||
| + | |||
| + | To run the '''lqr_BC_optimizer''', change the initial conditions(line 16-21) and the Q & R matrices(lines 51,52), then click Run. The output will be in the command window. | ||
| + | |||
| + | To run the '''runBicycleTest''', type in runBicycleTest(x0,y0,v0,delta0,phi0,phi_dot0,psi0, K, delta_offset, numTimeSteps, graph) into the command window and hit ENTER. The K values would ideally be the best gain values from lqr_BC_optimizer. The rest of the inputs are described below. Do not change anything in the file. Do not click anything while the test runs or else the plots/animation could become corrupted. | ||
| + | |||
| + | To run '''plotMultipleControllersTogether''', edit lines 3-6 to reflect the controllers you want to compare. If you need to, change the rest of the lines if you want to compare values other than lean,lean_rate,steer, & steer_rate. Make sure to edit them for every single controller or else your graphs won't make sense. | ||
| + | |||
=Commonly Used Variables= | =Commonly Used Variables= | ||
| − | *state: state is an vector with 8 state variables, in order they are, time step, X position, Y position, Lean Angle, Yaw Angle, Steer Angle, Lean Angle Rate, Velocity | + | *'''state''': state is an vector with 8 state variables, in order they are, time step, X position, Y position, Lean Angle, Yaw Angle, Steer Angle, Lean Angle Rate, Velocity |
| − | *motCommands - this is the same as <math>\vec{u}</math> in the control equation, for forward moving balancing, it is steer angle rate <math>[\dot{\delta}]</math> | + | *'''motCommands''' - this is the same as <math>\vec{u}</math> in the control equation, for forward moving balancing, it is steer angle rate <math>[\dot{\delta}]</math> |
| − | + | *'''K''' - this is the vector of the three gain values k1,k2,k3. They are used to find the value of <math>[\dot{\delta}]</math> | |
| − | == | + | |
| − | + | ||
| − | + | = MATLAB files = | |
| − | + | ||
| − | + | == '''lqr_BC_optimizer.m''' == | |
| − | + | This script calculates optimal gain values. For a specified set of initial conditions, this file runs the LQR algorith on a Q matrix, and then the scaled values of that Q matrix. Then it calls runBicycleTest on each of the sets of gain values that it calculates. Based on the outputs of runBicycleTest it knows whether the bike balanced or didn't from the success output of runBicycleTest. Then it uses the allStates and applies a balance score equation and path score equation to score how well those gain values worked. Then it prints out the optimal gain values based on the balance score and stores all the data into a csv file. | |
| − | + | ||
| − | + | ||
| − | + | =='''balanceControlOptimizer.m'''== | |
| − | + | This is an older script used to find optimal gain values. Instead of using LQR to find gain values to test, you manually input a range of gain values you want to test. Then the code tests these values the same way lqr_BC_optimizer does. | |
| − | + | ||
| − | + | ||
| − | + | == '''runBicycleTest.m''' == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | ||
Inputs: | Inputs: | ||
| − | * x0,y0 - | + | <div style="column-count:3;-moz-column-count:3;-webkit-column-count:3"> |
| + | * x0,y0 - initial location | ||
* v0 - initial speed | * v0 - initial speed | ||
| − | * delta0 - | + | * delta0 - initial steer angle |
| − | * phi0 - | + | * phi0 - initial lean angle |
| − | * phi_dot0 - | + | * phi_dot0 - initial lean angle ratw |
| − | * psi0 - | + | * psi0 - initial yaw angle (heading) |
* K - vector of gains (k1, k2, k3) | * K - vector of gains (k1, k2, k3) | ||
* delta_offset - either a scalar (a constant offset), or a vector of offsets (the bike will attempt to hit delta_offset(n) at the nth timestep | * delta_offset - either a scalar (a constant offset), or a vector of offsets (the bike will attempt to hit delta_offset(n) at the nth timestep | ||
* numTimeSteps - the number of time steps to run the simulation for | * numTimeSteps - the number of time steps to run the simulation for | ||
| − | * graph - 1= | + | * graph - 1=draws graph, 0=does not |
| − | === testSteerOffset.m == | + | </div> |
| + | |||
| + | |||
| + | Outputs: | ||
| + | *success - 1 if bike stayed up successfully throughout duration of the test, 0 if the bike falls down(lean angle becomes greater than pi/4 during the test) | ||
| + | *AllStates - matrix with size (number of time steps x 8). Each row of this matrix contains a state, it contains all the states for all the timesteps in the test. | ||
| + | |||
| + | |||
| + | This function uses state variables and gains and passes them to rhs, which produces the derivative of all the state variables(minus timestep) and the motor command then it uses that derivative and euler integrates to find the next state values. It repeats this process for all the time steps in the test. Each time step is 1/50 second apart. Finally it uses all the states and all the motor commands and calls animateBike, to produce an animation of the bike and create all the data graphs for analysis. runBicycleTest produces the p parameter used in rhs and animateBike. | ||
| + | |||
| + | |||
| + | == '''rhs.m''' == | ||
| + | Inputs: | ||
| + | <div style="column-count:3;-moz-column-count:3;-webkit-column-count:3"> | ||
| + | * currentState - contains the 8 current state variables | ||
| + | * p - contains bike parameters gravity, length of wheel base, distance from rear wheel to COM, height of COM, trail, and pause length | ||
| + | * K - Gain values | ||
| + | * delta_offset - desired steer angle | ||
| + | * phi_offset - desired lean angle | ||
| + | </div> | ||
| + | |||
| + | Outputs: | ||
| + | *zdot - zdot is a vector of the 7 derivatives of the state variables(minus timestep), it is used in the euler integration in runBicycleTest | ||
| + | *u - u is the same as the motor command, it is the <math>[\dot{\delta}]</math> that will be applied to the bike so that the bike can balance itself | ||
| + | |||
| + | |||
| + | rhs works by using the gains values to calculate u, and then using the EOM<ref>Shihao Wang. Dynamic model derivation and controller design for an autonomous bicycle. Dec 18 2014. https://drive.google.com/file/d/0ByhwjGqiUphVWmRETXZHb1ZZSlU/view</ref> to calculate the derivatives. It also sets a max steer angle rate to 4.8 rad/s based on the limitations of the motor used. For straight line balancing, delta_offset and phi_offset will be 0. For turning balancing, they will be determined by the navigation controller. rhs calls no other functions. | ||
| + | |||
| + | |||
| + | == '''BikeAndMotorConstants.m''' == | ||
| + | No inputs | ||
| + | Output: CONST - A vector containing important constants about the bike | ||
| + | |||
| + | |||
| + | This function calculates important constants including moment of inertia, center of mass, and others. It is called in drawBike. | ||
| + | |||
| + | |||
| + | == '''animateBike.m''' == | ||
| + | Inputs: | ||
| + | <div style="column-count:3;-moz-column-count:3;-webkit-column-count:3"> | ||
| + | * state - this is not one set of state variables, it is actually the allStates variable from runBicycleTest | ||
| + | * p - contains bike parameters gravity, length of wheel base, distance from rear wheel to COM, height of COM, trail, and pause length | ||
| + | * motCommands - steer angle rate. See above. | ||
| + | * delta_offset - desired steer angle | ||
| + | * phi_offset - desired lean angle | ||
| + | </div> | ||
| + | |||
| + | No Outputs | ||
| + | |||
| + | animateBike produces graphs and an animation of the bike test being run. Graphs produced: Lean vs Time, Lean Rate vs Time, Steer vs Time, Steer Rate vs Time, Steer Rate vs Time, X Position vs Y Position, Yaw Rate vs Time. | ||
| + | animate Bike calls drawBike repeatedly, once for each state. In between states it pauses for timestep length(1/50 sec). Inside a for loop, the 3-d plot containing drawBike is updated repeatedly making the animation. On each timestep, the location of the back wheel is added as a red dot to the ground. These add up to make a line that represents the trajectory of the bike. In the picture below you can see a frame of the animation. | ||
| + | |||
| + | |||
| + | == '''drawBike.m''' == | ||
| + | Inputs: | ||
| + | <div style="column-count:3;-moz-column-count:3;-webkit-column-count:3"> | ||
| + | * x - X position | ||
| + | * y - Y position | ||
| + | * z - Z position | ||
| + | * yaw - Yaw angle (heading) | ||
| + | * roll - Roll angle (lean angle) | ||
| + | * steer - Steer angle | ||
| + | * p - contains bike parameters gravity, length of wheel base, distance from rear wheel to COM, height of COM, trail, and pause length | ||
| + | </div> | ||
| + | |||
| + | |||
| + | Outputs: | ||
| + | *COG_hand - plots the center of gravity | ||
| + | *SH_hand - plots the handle bar | ||
| + | *CPfw_hand - plots the front wheel | ||
| + | *CPrq_hand - plots the back wheel | ||
| + | |||
| + | |||
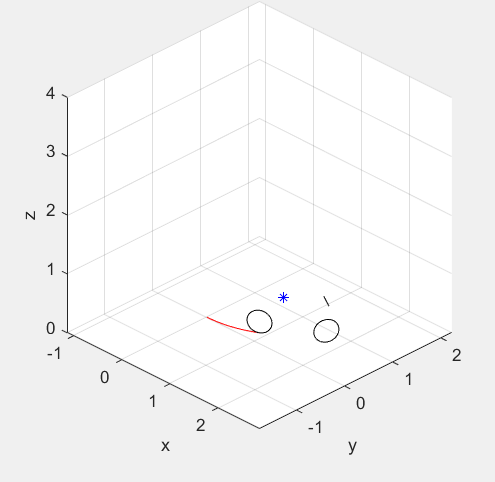
| + | This function uses state values to draw the bike at a single state, animateBike utilizes successions of these frames to make an animation. This function calls BikeAndMotorConstants to get center of mass and size dimensions to proportionally base the drawing on. It also cals CircleAboutZ to draw the circles for the wheels. The picture below shows a drawing of the bike in an animation. The line is the handle bars, the two circles are the wheels, and the blue star is the center of mass. The red line is produced by animateBike and is the trajectory that has already been travelled by the bike. | ||
| + | |||
| + | [[File:BikeAnimation.PNG|500px|center]] | ||
| + | <br clear=all> | ||
| + | |||
| + | |||
| + | |||
| + | == '''CircleAboutZ.m''' == | ||
| + | Inputs: | ||
| + | * r - radius of the circle | ||
| + | |||
| + | Outputs: | ||
| + | * CP - vector containing x and y values of a circle of radius r based around the origin. The z values are all 0, so the circle exists in the xy plane. | ||
| + | |||
| + | This function simply uses cosine and sine to find the x and y values for a circle using 100 theta values between 0 and 2pi. These values are used in drawBike to draw the wheels. The radius for the wheels is determined by BikeAndMotorConstants which is called in drawBike. | ||
| + | |||
| + | |||
| + | == '''plotMultipleControllersTogether.m''' == | ||
| + | This script runs runBicycleTest four times using different parameters. The user inputs the different parameters, then it makes plots comparing the four different parameters. Ideally you would only change the gain values on the parameters to compare the gains. It creates plots for Lean vs Time, Lean Rate vs Time, Steer vs Time, & Steer Rate vs Time. Make sure you put 0 as the graph parameter for runBicycleTest so the animation and plots don't appear for every single instance. | ||
| + | |||
| + | |||
| + | == '''testSteerOffset.m''' == | ||
| + | For our straight line balance the steer offset desired is 0. But for navigation it will be constantly changing. This script tests how well a set of gain values performs when the desired steer angle changes sinusoidally. The user inputs four different gains vectors, then the script runs runBicycleTest for each gain vector with the sinusoidal delta_offset. Then it graphs the four controllers against each other for Lean vs Time, Lean Rate vs Time, Steer vs Time, Steer Rate vs Time, Bicycle Trajectory, & Yaw Rate vs Time. The script also creates a score for how well the the bike achieved the desired steer angle. It prints out these scores, or if the bike fell, it prints out that the test failed. | ||
| + | |||
| + | |||
| + | |||
== See also == | == See also == | ||
* [[LQR]] | * [[LQR]] | ||
| + | |||
| + | == References == | ||
Latest revision as of 01:06, 18 May 2020
What are these files for?
The find a good controller, you must find good gains values for the controller. This is easier said than done. The LQR function of matlab helps us to find the best gains values for two given cost matrices. But manually testing them is a lot of work, so the LQR file we have runs the LQR algorithm on many different cost matrix values and then also runs tests on each set of gains values to give you the best one possible. Running those tests requires a few different files. Once you have decided on a set of gains values that you want to explore more. You can run a singular test with those using runBicycleTest. The test will run telling you whether the bike fell or not, but it will also animate the bike and create multiple plots. This is needed to get a better insight on to how your controller is performing. When you have decided on a few different controllers you think perform well, you can run them individually and compare everything in detail, or you can run the plotMultipleControllersTogether file to run tests on those controllers and create plots comparing the controllers.
How To Run Them
To run the lqr_BC_optimizer, change the initial conditions(line 16-21) and the Q & R matrices(lines 51,52), then click Run. The output will be in the command window.
To run the runBicycleTest, type in runBicycleTest(x0,y0,v0,delta0,phi0,phi_dot0,psi0, K, delta_offset, numTimeSteps, graph) into the command window and hit ENTER. The K values would ideally be the best gain values from lqr_BC_optimizer. The rest of the inputs are described below. Do not change anything in the file. Do not click anything while the test runs or else the plots/animation could become corrupted.
To run plotMultipleControllersTogether, edit lines 3-6 to reflect the controllers you want to compare. If you need to, change the rest of the lines if you want to compare values other than lean,lean_rate,steer, & steer_rate. Make sure to edit them for every single controller or else your graphs won't make sense.
Commonly Used Variables
- state: state is an vector with 8 state variables, in order they are, time step, X position, Y position, Lean Angle, Yaw Angle, Steer Angle, Lean Angle Rate, Velocity
- motCommands - this is the same as in the control equation, for forward moving balancing, it is steer angle rate
- K - this is the vector of the three gain values k1,k2,k3. They are used to find the value of
MATLAB files
lqr_BC_optimizer.m
This script calculates optimal gain values. For a specified set of initial conditions, this file runs the LQR algorith on a Q matrix, and then the scaled values of that Q matrix. Then it calls runBicycleTest on each of the sets of gain values that it calculates. Based on the outputs of runBicycleTest it knows whether the bike balanced or didn't from the success output of runBicycleTest. Then it uses the allStates and applies a balance score equation and path score equation to score how well those gain values worked. Then it prints out the optimal gain values based on the balance score and stores all the data into a csv file.
balanceControlOptimizer.m
This is an older script used to find optimal gain values. Instead of using LQR to find gain values to test, you manually input a range of gain values you want to test. Then the code tests these values the same way lqr_BC_optimizer does.
runBicycleTest.m
Inputs:
- x0,y0 - initial location
- v0 - initial speed
- delta0 - initial steer angle
- phi0 - initial lean angle
- phi_dot0 - initial lean angle ratw
- psi0 - initial yaw angle (heading)
- K - vector of gains (k1, k2, k3)
- delta_offset - either a scalar (a constant offset), or a vector of offsets (the bike will attempt to hit delta_offset(n) at the nth timestep
- numTimeSteps - the number of time steps to run the simulation for
- graph - 1=draws graph, 0=does not
Outputs:
- success - 1 if bike stayed up successfully throughout duration of the test, 0 if the bike falls down(lean angle becomes greater than pi/4 during the test)
- AllStates - matrix with size (number of time steps x 8). Each row of this matrix contains a state, it contains all the states for all the timesteps in the test.
This function uses state variables and gains and passes them to rhs, which produces the derivative of all the state variables(minus timestep) and the motor command then it uses that derivative and euler integrates to find the next state values. It repeats this process for all the time steps in the test. Each time step is 1/50 second apart. Finally it uses all the states and all the motor commands and calls animateBike, to produce an animation of the bike and create all the data graphs for analysis. runBicycleTest produces the p parameter used in rhs and animateBike.
rhs.m
Inputs:
- currentState - contains the 8 current state variables
- p - contains bike parameters gravity, length of wheel base, distance from rear wheel to COM, height of COM, trail, and pause length
- K - Gain values
- delta_offset - desired steer angle
- phi_offset - desired lean angle
Outputs:
- zdot - zdot is a vector of the 7 derivatives of the state variables(minus timestep), it is used in the euler integration in runBicycleTest
- u - u is the same as the motor command, it is the that will be applied to the bike so that the bike can balance itself
rhs works by using the gains values to calculate u, and then using the EOM[1] to calculate the derivatives. It also sets a max steer angle rate to 4.8 rad/s based on the limitations of the motor used. For straight line balancing, delta_offset and phi_offset will be 0. For turning balancing, they will be determined by the navigation controller. rhs calls no other functions.
BikeAndMotorConstants.m
No inputs Output: CONST - A vector containing important constants about the bike
This function calculates important constants including moment of inertia, center of mass, and others. It is called in drawBike.
animateBike.m
Inputs:
- state - this is not one set of state variables, it is actually the allStates variable from runBicycleTest
- p - contains bike parameters gravity, length of wheel base, distance from rear wheel to COM, height of COM, trail, and pause length
- motCommands - steer angle rate. See above.
- delta_offset - desired steer angle
- phi_offset - desired lean angle
No Outputs
animateBike produces graphs and an animation of the bike test being run. Graphs produced: Lean vs Time, Lean Rate vs Time, Steer vs Time, Steer Rate vs Time, Steer Rate vs Time, X Position vs Y Position, Yaw Rate vs Time. animate Bike calls drawBike repeatedly, once for each state. In between states it pauses for timestep length(1/50 sec). Inside a for loop, the 3-d plot containing drawBike is updated repeatedly making the animation. On each timestep, the location of the back wheel is added as a red dot to the ground. These add up to make a line that represents the trajectory of the bike. In the picture below you can see a frame of the animation.
drawBike.m
Inputs:
- x - X position
- y - Y position
- z - Z position
- yaw - Yaw angle (heading)
- roll - Roll angle (lean angle)
- steer - Steer angle
- p - contains bike parameters gravity, length of wheel base, distance from rear wheel to COM, height of COM, trail, and pause length
Outputs:
- COG_hand - plots the center of gravity
- SH_hand - plots the handle bar
- CPfw_hand - plots the front wheel
- CPrq_hand - plots the back wheel
This function uses state values to draw the bike at a single state, animateBike utilizes successions of these frames to make an animation. This function calls BikeAndMotorConstants to get center of mass and size dimensions to proportionally base the drawing on. It also cals CircleAboutZ to draw the circles for the wheels. The picture below shows a drawing of the bike in an animation. The line is the handle bars, the two circles are the wheels, and the blue star is the center of mass. The red line is produced by animateBike and is the trajectory that has already been travelled by the bike.
CircleAboutZ.m
Inputs:
- r - radius of the circle
Outputs:
- CP - vector containing x and y values of a circle of radius r based around the origin. The z values are all 0, so the circle exists in the xy plane.
This function simply uses cosine and sine to find the x and y values for a circle using 100 theta values between 0 and 2pi. These values are used in drawBike to draw the wheels. The radius for the wheels is determined by BikeAndMotorConstants which is called in drawBike.
plotMultipleControllersTogether.m
This script runs runBicycleTest four times using different parameters. The user inputs the different parameters, then it makes plots comparing the four different parameters. Ideally you would only change the gain values on the parameters to compare the gains. It creates plots for Lean vs Time, Lean Rate vs Time, Steer vs Time, & Steer Rate vs Time. Make sure you put 0 as the graph parameter for runBicycleTest so the animation and plots don't appear for every single instance.
testSteerOffset.m
For our straight line balance the steer offset desired is 0. But for navigation it will be constantly changing. This script tests how well a set of gain values performs when the desired steer angle changes sinusoidally. The user inputs four different gains vectors, then the script runs runBicycleTest for each gain vector with the sinusoidal delta_offset. Then it graphs the four controllers against each other for Lean vs Time, Lean Rate vs Time, Steer vs Time, Steer Rate vs Time, Bicycle Trajectory, & Yaw Rate vs Time. The script also creates a score for how well the the bike achieved the desired steer angle. It prints out these scores, or if the bike fell, it prints out that the test failed.
See also
References
- ↑ Shihao Wang. Dynamic model derivation and controller design for an autonomous bicycle. Dec 18 2014. https://drive.google.com/file/d/0ByhwjGqiUphVWmRETXZHb1ZZSlU/view

![{\displaystyle [{\dot {\delta }}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31b15d35307788dd9ebf95634860a37c0fe7b192)